En la entrada de hoy les proponemos un reto dirigido a los aficionados a la ingeniería inversa.
Para participar, pueden descargar el siguiente binario. Se trata de un ejecutable PE para Windows 32-bit que contiene un algoritmo de validación de números de serie:
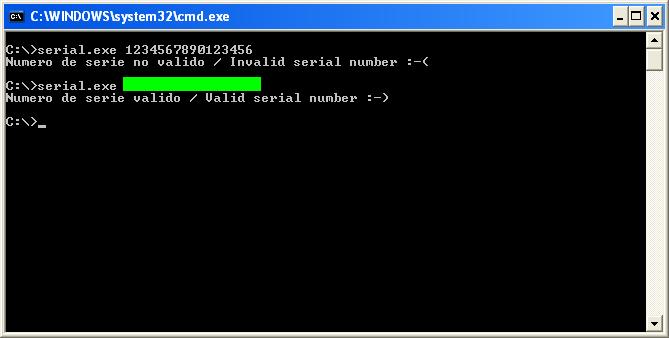
Los números de serie están formados por 16 dígitos numéricos, pudiendo tomar cada uno de ellos un valor entre 0 y 9. El objetivo del reto es obtener un número de serie válido sin modificar el binario (es decir, se trata de obtener la segunda de las salidas del pantallazo anterior sin necesidad de manipular el programa; tan sólo hallando el mecanismo de validación con ingeniería inversa).
Esperamos que disfruten del reto. ¡Un saludo!
Enlaces de interés:

He pasado un rato entretenido con el reto.
Aquí os dejo un keygen en python.
http://pastebin.com/ZuV5raYf [pastebin.com][ZuV5raYf]
Enhorabuena Rubén!
Te me has adelantado :-)
Yo únicamente pensaba colocar el serial (0430400527053331) pero al ver tu solución me he animado a escribir un script en python también (me gusta más el tuyo de todas formas).
Un saludo
88
C:\>serial.exe 0430400527053331
Numero de serie valido / Valid serial number :-)
# cat serial.py
#!/usr/bin/python
check = [0,4,6,0,6,0,0,5,6,3,0,5,6,9,2,5]
solution = “”
for i in range(16):
for j in range(10):
if i*j % 10 == check[i]:
solution += str(j)
break
print solution
# ./serial.py
0430400527053331
¡Qué rapidez! Felicidades a los que habéis dado con la solución. Añado una pequeña aportación dándole una vuelta de tuerca: observando la fórmula y los valores que deben hallarse para aceptar cada dígito resulta obvio que existe más de un serial que puede ser dado por bueno, en concreto existen 16000 posibles seriales. Los números que cumplen las condiciones exigidas para cada posición son:
Posición 0: 0 1 2 3 4 5 6 7 8 9
Posición 1: 4
Posición 2: 3 8
Posición 3: 0
Posición 4: 4 9
Posición 5: 0 2 4 6 8
Posición 6: 0 5
Posición 7: 5
Posición 8: 2 7
Posición 9: 7
Posición 10: 0 1 2 3 4 5 6 7 8 9
Posición 11: 5
Posición 12: 3 8
Posición 13: 3
Posición 14: 3 8
Posición 15: 1 3 5 7 9
De la combinación de todos ellos obtenemos los 16000 serials diferentes. Dejo un programilla C# en GitHub que realiza el cálculo y muestra todas las combinaciones posibles: https://github.com/EduardMillan/Security-Artwork-Serial
¡Enhorabuena! Me alegro de que hayais pasado un rato entretenido destripando el reto :-)
*** ¡¡ATENCIÓN!! SPOILERS ***
La fórmula viene dada por el siguiente código en ensamblador:
loadi 3 1
loadi 4 0
loadi 5 17
loadi 6 17
loadi 7 33
loadi 8 0
load 0 4
mul 0 4
load 2 5
eq 0 2
add 4 3
add 5 3
jneq 48 0
eq 4 6
jeq 54 0
jmp 18 0
store 7 8
halt 0 0
store 7 3
halt 0 0
Por supuesto, se trata del ensamblador de una CPU ficticia, inventada para la ocasión ;-)
Es traducido (“ensamblado”) por un script en Python (asm.py) al siguiente “código máquina” en C:
#define LOADI 53
#define LOAD 92
#define ADD 56
#define JEQ 90
#define HALT 69
#define MUL 77
#define JNEQ 15
#define EQ 44
#define JMP 22
#define STORE 89
int I[] = {
53, 3, 1,
53, 4, 0,
53, 5, 17,
53, 6, 17,
53, 7, 33,
53, 8, 0,
92, 0, 4,
77, 0, 4,
92, 2, 5,
44, 0, 2,
56, 4, 3,
56, 5, 3,
15, 48, 0,
44, 4, 6,
90, 54, 0,
22, 18, 0,
89, 7, 8,
69, 0, 0,
89, 7, 3,
69, 0, 0,
};
A continuación, el programa serial.exe emula este código máquina, ejecutando la fórmula correspondiente (podeis ver el código: serial.c).
Por supuesto, la fórmula podría haber sido más compleja (incluso se podría haber escrito una fórmula complicada en un lenguaje de alto nivel como C y después “compilado” este código al ensamblador de la máquina emulada), pero espero haber acertado con el nivel de dificultad para que el reto fuera medianamente interesante pero no “imposible”.
Muchas gracias a todos por leer el blog y participar en el reto.
Menudo equipo de expertos tenéis por aquí jejeje. Vista la rapidez con que lo han sacado, igual conviene subir un peldaño más en el próximo reto.