Fundamentos sobre certificados digitales (VI) – Algoritmos Criptográficos

En nuestra entrada respecto a certificados digitales de este mes, nos vamos a centrar en un punto crítico dentro de la infraestructura de una PKI. Este tema se ha ido comentando leve y superficialmente en anteriores entradas; sin embargo, se trata de uno de los puntos más importantes que está afecta directamente con los propios a la construcción de los propios certificados y tiene una dependencia directa con la robustez de los mismos; este punto es el referente a algoritmos criptográficos.

Como introducción y a modo de repaso, un certificado digital no es ni más ni menos que un par de claves de criptografía asimétrica que, empleando las propiedades de las mismas, permiten identificar inequívocamente a una persona, entidad o website (en el caso de certificados SSL). Más información y detalle de esto en la entrada Fundamentos sobre certificados digitales I y II.

Las claves criptográficas se generan empleando algoritmos criptográficos, lo que propicia como ya se comentó, que cada clave empleada y cualquier información cifrada están directamente relacionadas mediante una relación matemática. Esto significa que siempre se conoce el método para obtener la clave privada correspondiente a una clave pública y viceversa (disponiendo de mensajes cifrados con las mismas). Entonces, ¿que impide a un tercero obtener la clave privada de alguien?, ¿cómo se puede asegurar la identidad de alguien únicamente basándonos en que posea una clave privada que aparentemente no es segura?

Los algoritmos de cifrado aprovechan operaciones que son sencillas de aplicar y que son extremadamente complejas de deshacer. Entiendo que este hecho es difícil de comprender, pero está directamente relacionado con la tecnología de cómputo actual y los métodos numéricos a nuestra disposición. Me explico: aunque el cómputo sea conocido y realizable, el hecho determinante es si se dispone de un método de resolución lineal y los mismos están implementados en hardware. Sin embargo, en los algoritmos de cifrado se aprovecha el hecho de que, con la tecnología y conocimiento existente en el momento en el que se diseñan, el tiempo de cómputo necesario para realizar las operaciones que permiten obtener una de las claves basándonos en la otra es, con mucho, más complejo que el necesario para generarlas y más largo que la propia vida del certificado.

Evidentemente y como más de uno ya habrá pensado, este hecho es relativo. Como es bien sabido, la tecnología avanza a pasos agigantados año tras año, y evidentemente no se disponía de la misma potencia de cálculo hace 20 años que ahora, ni se dispondrá de la misma potencia de cálculo ahora que dentro de 20. Del mismo modo, es posible que en el tiempo, se descubran métodos para resolver cómputo relacionado con el algoritmo de una forma más eficiente. Los hechos relatados hacen que un algoritmo que se considera seguro en un momento pueda dejar de serlo pasado un tiempo.

Un ejemplo conocido de este hecho es el algoritmo DES, que no se emplea para generación de claves asimétricas, pero sí para cifrado. En este caso, el algoritmo DES genera una clave, que es la que se emplea en el cifrado y el descifrado de la información.

El algoritmo DES surgió oficialmente el año 1975 y llegó a ser un estándar de facto de cifrado. De forma sencilla y omitiendo algunos detalles, el algoritmo DES es básicamente un algoritmo de cifrado por bloques: se ejecutan 16 fases idénticas de proceso denominadas rondas y en cada una de ellas se ejecuta la misma función (función de Feistel). Desde finales de los 70 hasta principios de los 90 aparecieron distintos grupos de investigadores que propusieron vulnerabilidades teóricas del algoritmo basadas en su criptoanálisis y se propusieron diversos modelos de máquinas para poder descifrar una clave DES en un tiempo razonable. Dichas máquinas eran inviables económica y técnicamente en los primeros años pero fueron yendo viables poco a poco conforme pasaban los mismos. Finalmente se demostró una de las vulnerabilidades del algoritmo en 1998, cuando se diseñó y construyó una máquina de propósito específico que fue capaz de obtener una clave DES basándose en datos cifrados en 2 días, sin desmerecer el trabajo de criptoanálisis realizado, fue la tecnología disponible en el momento para descifrar el algoritmo ya que, si el trabajo se realizó en dos días en 1998, ello implica que con la potencia de cálculo actual se descifraría la información en mucho menos tiempo.

Una vez puestos en contexto y pasando directamente a la materia que nos ocupa, si existe un algoritmo determinante en el uso de la criptografía en firma y certificado digital es el algoritmo RSA. El algoritmo se describe, de forma breve, como un algoritmo de clave asimétrica por bloques, y su robustez se basa en la complejidad computacional que requiere realizar una descomposición en factores primos de un número exponencialmente grande. Una descomposición de factores primos consiste en obtener de un número el conjunto de números primos que multiplicados de por sí dan dicho número. Este problema con números pequeños es sencillo de solucionar; más de uno se habrá acordado de sus tiempos en el colegio realizando descomposiciones en factores primos de números de dos y tres cifras. Sin embargo, este mismo problema con un número de cientos de cifras es muy complejo de resolver.

Un par de claves RSA, pública y privada, están formadas por dos partes diferenciadas denominadas módulo (n) y exponente (ec y ed). El módulo es común a ambas claves y el exponente es distinto en cada caso, empleándose el exponente de cifrado en la clave pública y el exponente de descifrado en la privada. Dichas partes tienen un propósito distinto dentro del cifrado y descifrado de la información.

Para la generación del módulo de las claves se deben seleccionar un par de números primos, la complejidad del cifrado dependerá directamente de la longitud de dichos números, por lo que por motivos de seguridad deberán seleccionarse aleatoriamente y deberán tener una longitud mínima.

Por otra parte, el cálculo de los exponentes se realiza basándose en relaciones matemáticas basadas en la función de Euler de los dos números primos originales. Estas relaciones permiten que ambos exponentes y el módulo cumplan con su función para el cifrado y descifrado.

Una vez se dispone de ambas claves, se puede realizar el cifrado y descifrado de la firma o información a enviar, para ello voy a recurrir a un sencillo ejemplo. Teniendo un mensaje M, el mismo se convierte mediante un protocolo pre acordado y reversible en un número entero m, sobre el que se implementará el cifrado. Dadas dos claves, una pública pub(n,ec), formadas por su módulo y exponente de cifrado y una clave privada priv(n,ed), formadas por su módulo y exponente de descifrado; el cifrado se aplicará con la siguiente fórmula:

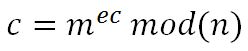
Siendo c el mensaje cifrado que se podría transmitir sin riesgos. Se calcula la potencia del mensaje por el exponente de cifrado y se calcula el resto de su división por el módulo de la clave (dicha operación se denomina módulo, valga la redundancia). Ese último valor es el mensaje cifrado. Por su lado el descifrado se realiza del siguiente modo:

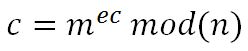
Una vez recibido y descifrado el mensaje con un método semejante al del cifrado, se volvería a aplicar el protocolo pre acordado para obtener el mensaje original M a partir de su número entero equivalente m. Esta relación es posible gracias a las propiedades matemáticas que se mencionan en la creación de los exponentes.

Como es obvio, el objetivo de un atacante que quiera suplantar la identidad de alguien empleando su certificado digital será obtener el exponente de descifrado dado que el módulo de la clave es común con la clave pública. Dado que los exponentes se calculan empleando los números primos originales que constituyen el módulo, para romper el cifrado se deberá factorizar el módulo para encontrarlos. Al ser el método de cifrado público, una vez obtenidos dichos números se podría generar ambas claves.

Como se ha podido observar las operaciones que se realizan en el cifrado y descifrado son relativamente simples, un detalle importante para la viabilidad de uso de un protocolo; del mismo modo, y a pesar de que no se ha entrado en detalles, las operaciones necesarias para obtener las claves RSA son más complejas que las de cifrado y descifrado, pero son exponencialmente más sencillas que las asociadas a la operación inversa, que requiere la factorización de números muy grandes.

La longitud de la clave RSA será por tanto la suma de las longitudes de módulo y cualquiera de los exponentes. Esta longitud se establece en bits y la seguridad del cifrado es directamente proporcional a la longitud de su clave, ya que la clave será más larga cuando más grande sea el número a factorizar. Lo habitual y recomendable en la actualidad es emplear claves de 2048 bits de longitud (lo que se traduce en emplear números primos de unas 617 cifras aproximadamente para calcular el módulo). Como es obvio, estos criterios se revisarán con el paso del tiempo y dependerán de la potencia de cómputo, así como de las vulnerabilidades o métodos que se puedan aplicar en el protocolo.

El método criptográfico empleado es fundamental para implantar criptografía de clave pública o cualquier otro método de cifrado, ya que determina específicamente la robustez del sistema implementado.

Con esto es todo, espero haber podido daros un poco de idea de qué es la criptografía y como funciona, así como cómo se aplica en certificados y firmas digitales. Espero que la entrada no haya resultado demasiado extensa ni demasiado compleja, ya que se trata de una materia que entiendo que para muchos puede ser algo aburrida. Muchas gracias por leernos como siempre, próximamente más entregas de esta serie.